- Докладчик: Вонти А.О.
- Тема: Методы контроля разрешающей способности матричных фотоприемников.
- Организация: АО «НПП «Элар»
Разрешающая способность является важной характеристикой матричных фотоприёмников, однако измерение этой характеристики является сложной и неоднозначной задачей. Существует несколько параметров, характеризующих пространственное разрешение и достаточно много различных методик их измерения, применимых в определенных условиях. Под термином «разрешающая способность» чаще всего понимают два разных параметра – КПК (коэффициент передачи контраста) и ФПМ (функция передачи модуляции). Так или иначе, при измерении важны точность и воспроизводимость метода.
Измерение КПК и его частотная зависимость – ЧКХ (Contrast Transfer Function – CTF, частотно-контрастная характеристика) является более простым в реализации методом оценки разрешающей способности, поскольку КПК представляет собой амплитуду отклика системы на воздействие тестового оптического сигнала в виде прямоугольной миры – чередующихся черно-белых полос равной ширины (меандровый сигнал), которые сравнительно просто воспроизводятся. Однако КПК может быть использован для оценки разрешающей способности только одной части оптического тракта, так как меандровый сигнал обладает сложным пространственным спектром и отдельные его компоненты имеют разный коэффициент пропускания для любого из звеньев оптичесокого тракта.
С другой стороны, ФПМ (MTF – Modulation Transfer Function) равна амплитуде (модулю) комплексного коэффициента пропускания системы при синусоидальном входном воздействии с заданной пространственной частотой. У синусоидального сигнала при прохождении разных звеньев видеотракта меняется только фаза и амплитуда, а частота остается неизменной.
В докладе рассмотрена методика измерения ФПМ на основе методики описанной в ISO 12233- 2000 (международная организации по стандартизации), в которой используется наклонный оптический нож (черно-белый перепад с единственной прямой кромкой), который не так сложен в изготовлении как тест-таблицы с синусоидальным распределением плотности. Также при использовании наклонного ножа не требуются прецизионные подвижки с субмикронным разрешением как в случае использования вертикального или горизонтального оптического ножа.
Метод был дополнен формированием оптической маски непосредственно на поверхности фотоприемной матрицы (в технологическом процессе изготовления кристаллов фотоприемников на пластине), чтобы исключить неопределенность, вносимую проекционной оптической системой и избежать сложных (и зачастую неоднозначных) процедур для её метрологической аттестации. Минусом методики с использованием оптического ножа на поверхности фоточувствительной матрицы является влияние качества нанесенного ножа на точность получаемых данных, а также невозможность неразрушающей оценки разрешения на каждом приборе.
Для обработки полученных результатов был разработан алгоритм, написанный на языке Python. В предшествующей работе результаты обрабатывались в программе Excel, где полученная ESF (Edge Spread Function) подвергалась сглаживанию, и это вносило ошибку в вычисления, в Python сглаживание не требуется, а также обработка в Python менее трудоемкая и более быстрая.
Обработка данных включает следующие шаги:
- Построение ESF (Edge Spread Function — функция отклика на ступень) из полученных данных с выходного устройства ФПЗС.
- Вычисление первой производной от ESF – LSF (Linear Spread Function), описывающую отклик ячейки на дельта-воздействие, то есть её координатную характеристику.
- Выполнение преобразования Фурье функции LSF, и взятие модуля от комплексных значений.
В 2019 году была завершена работа по разработке, изготовлению и поставке ФПЗС ВЗН с ячейкой 9 мкм. На Рисунке 1 показаны полученные графики с прибора, со сформированным на фоточувствительной поверхности оптическим ножом, при падающем излучении длиной волны 500нм. Цифры соответствуют шагам обработки:
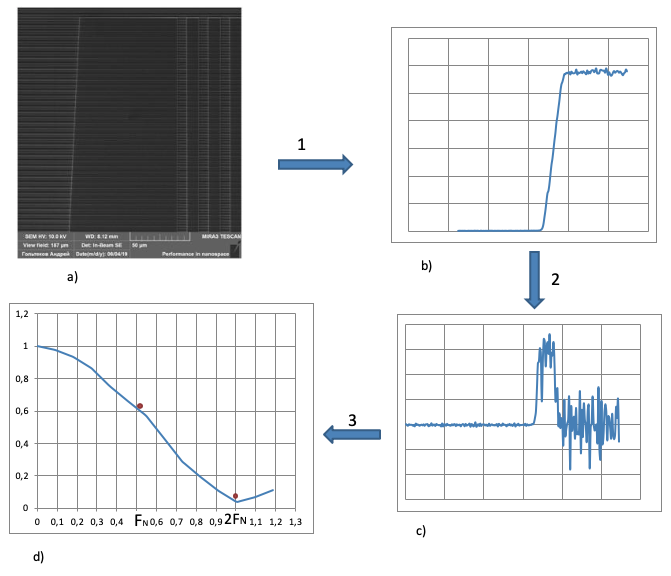
Также были получены зависимости ФПМ от длины волны излучения падающего на микросхему.
Длина волны, нм | ФПМ на частоте Найквиста | Длина волны, нм | ФПМ на частоте Найквиста | Длина волны, нм | ФПМ на частоте Найквиста |
400 | 0.52 | 620 | 0.50 | 840 | 0.21 |
420 | 0.61 | 640 | 0.46 | 860 | 0.20 |
440 | 0.62 | 660 | 0.43 | 880 | 0.19 |
460 | 0.63 | 680 | 0.41 | 900 | 0.18 |
480 | 0.63 | 700 | 0.37 | 920 | 0.17 |
500 | 0.62 | 720 | 0.35 | 940 | 0.16 |
520 | 0.61 | 740 | 0.32 | 960 | 0.15 |
540 | 0.59 | 760 | 0.29 | 980 | 0.15 |
560 | 0.57 | 780 | 0.27 | 1000 | 0.15 |
580 | 0.55 | 800 | 0.25 |
|
|
600 | 0.52 | 820 | 0.23 |
|
|
Результаты показали свою устойчивость, воспроизводимость, адекватность в соответствии с математической моделью, а так же предсказуемость.
Зубков Василий Иванович
СПбГЭТУ «ЛЭТИ»
Вопрос:
В дискретном преобразовании Фурье под частотой Найквиста понимается максимальная частота, определяемая экспериментальными данными. В связи с этим, объясните появление удвоенной частоты Найквиста на рис. 1d? Или в работе не применяются преобразования Фурье? Еще, почему на рис.1d указаны всего только две точки? Через них можно провести любую кривую!
Вонти А.О.
Ответ:
Частота Найквиста — частота, равная половине частоты дискретизации. Соответственно, удвоенная частота Найквиста и есть частота дискретизации, в данном случае это частота синуса, который ровно «помещается» в ячейку матрицы. Следовательно, в данной работе мы получаем информацию вплоть до частоты дискретизации.
На рисунке отмечены только две точки, однако кривая состоит из множества точек, полученных из экспериментальных данных после математических преобразований.
